
空気抵抗がある自由落下の微分方程式をラプラス変換を使って解いてみました。ラプラス変換や微分方程式の例題として、自由落下は良い事例ではないかと思います。できるだけ丁寧に解説しますので、ラプラス変換による微分方程式の解法をマスターしていきましょう。
スポンサーリンク
基礎知識
空気抵抗がある自由落下の微分方程式を解くにあたって、理解しておきたい点が3点あります。
- 自由落下の力のつりあい
- 位置/速度/加速度と微分積分の関係
- ラプラス変換/ラプラス逆変換
①自由落下の力のつり合い
自由落下の力のつり合いについてですが、図のようにような関係になっています。
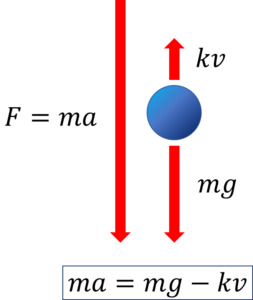
力の方向は下方向を正とするので、\(mg\)や加速度\(a\)の方向も下方向になります。
また、空気抵抗は落下速度に比例して強くなり\(kv\)と表すことができ、この力は上方向になります。
\(m\):質量 \(a\):加速度 \(g\):重力加速度 \(k\):空気抵抗係数 \(v\):落下速度
②位置/速度/加速度と微分積分の関係
位置・速度・加速度と微分積分の関係は以下のよう図のような関係になっています。
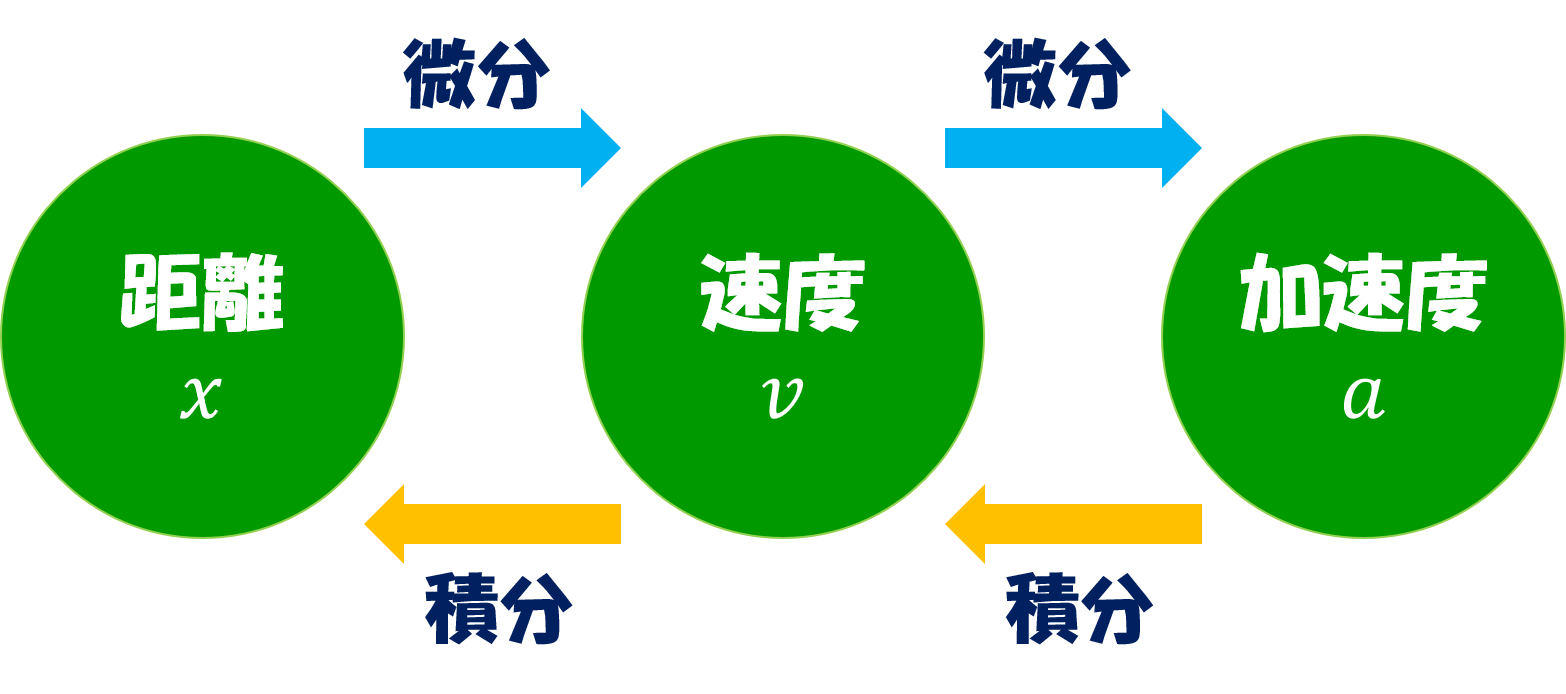
距離を微分すると速度になり、速度を微分すると加速度になります。また、加速度を積分すると速度になり、速度を積分すると距離になります。
また、数式で記述すると以下のような感じになります。

よって先ほどの力のつり合いの式は以下のように表現することも可能です。
加速度を基準とした場合
力のつり合いを\(a\)で表します。
$$ma(t) = mg – k\int_0^t a(τ)dτ $$
速度を基準とした場合
力のつり合いを\(v\)で表します。
$$m \frac{dv(t)}{dt}=mg – kv(t)$$
位置を基準とした場合
力のつり合いを\(x\)で表します。
$$m \frac{d^2x(t)}{dt^2}=mg – k\frac{dx(t)}{dt}$$
これら3つの式はすべて同じものです。
表現の仕方が違うだけなので、自由に変換できるように練習しておきましょう。
③ラプラス変換/ラプラス逆変換
今回は微分方程式をラプラス変換/ラプラス逆変換を用いて解くので、いくつか公式を覚えておく必要があります。ラプラス変換は時間\(t\)の関数を\(s\)空間に置き換えるために使用します。
ここに記載しているのはすべての公式ではないですが、今回の自由落下の解析に用いる公式を紹介します。
ラプラス変換の公式
| 元の関数 | ラプラス変換 |
| \(f(t)\) | \(F(s)\) |
| 1 | \(\frac{1}{s}\) |
| \(\int_0^t f(τ)dτ\) | \(\frac{1}{s} F(s)\) |
| \(\frac{df(t)}{dt}\) | \(sF(s)-f(0)\) |
| \(\frac{d^2f(t)}{dt^2}\) | \(s^2F(s)-sf(0)-f'(0)\) |
またラプラス逆変換は\(s\)空間を時間\(t\)の関数に戻すために使用します。ここで紹介するのは、下記2種類ですが、このラプラス逆変換は頻出なのでぜひ覚えておきましょう。
ラプラス逆変換の公式
| s関数 | ラプラス逆変換 |
| \(\frac{1}{s}\) | \(1\) |
| \(\frac{1}{s+a}\) | \(e^{-at}\) |
スポンサーリンク
加速度
それではまず加速度について解いていきたいと思います。
運動方程式は以下のように記述できます。ここで\((t)\)とは時間の関数で表されることを意味しています。つまり、加速度\(a\)と速度\(v\)は時間によって変化する関数ということです。
$$ma(t) = mg – kv(t)$$
今回は加速度\(a\)に関して解くので、\(a\)を使って表すと以下のようになります。
$$ma(t) = mg – k\int_0^t a(τ)dτ $$
ここで、この関数をラプラス変換を考えます。\(ma(t)\)は\(mA(s)\)となり、\(mg\)は\(\frac{mg}{s}\)となり、\( k\int_0^t a(τ)dτ\)は\(\frac{k}{s} A(s)\)となります。よって、
$$mA(s)=\frac{mg}{s}-\frac{k}{s} A(s)$$
となります。この変換ができない方は先ほど紹介したラプラス変換の公式を再確認してみてください。
これを\(A(s)\)について整理していきます。
$$msA(s)=mg-kA(s)$$
$$A(s)(ms+k)=mg$$
$$A(s)=\frac{mg}{ms+k}$$
分母の\(s\)の係数を1にしたいので\(m\)で割ります。
$$A(s)=\frac{g}{s+\frac{k}{m}}$$
ここまででラプラス変換での式変形は終了です。
今度はこの\(s\)の関数をラプラス逆変換を用いて時間\(t\)の関数に戻してあげます。
\(\frac{1}{s+a}\)⇒\(e^{-at}\)の公式を使うと以下のようになります。
$$a(t)=ge^{-\frac{k}{m} t}$$
\(t=0\)の時と\(t=∞\)の時の数値を確認しておきましょう。
\(t=0\)の時\(a(0)=g\)となり、落下し始めた瞬間の加速度が\(g\)になることが分かります。
また、\(t=∞\)の時\(a(∞)=0\)となり、十分な時間が経つと速度は収束し、加速はしないということが分かります。
このように\(t=0\)の時と\(t=∞\)の時だけでも数値を計算してみると、感覚的に答えが合っているかどうかがわかるので、検算する際は\(t=0\)の時と\(t=∞\)の時の数値を確認することをおすすめします。
速度
それでは次に速度について解いていきたいと思います。
運動方程式は先ほどと同じで以下の通りになります。
$$ma(t) = mg – kv(t)$$
今回は速度\(v\)に関して解くので、\(v\)を使って表すと以下のようになります。
$$m \frac{dv(t)}{dt}=mg – kv(t)$$
よって、この式をラプラス変換すると以下のように記述することができます。
$$m\{sV(s)-v(0)\}=\frac{mg}{s}-kV(s)$$
ここでもやはりラプラス変換の公式を使いますので、ラプラス変換ができない方は公式を見直してみましょう。
これを\(V(s)\)について整理すると以下のようになります。
$$V(s)=\frac{m\{g+sv(0)\}}{s(ms+k)}$$
この式のままではラプラス逆変換の公式は使えないので、部分分数分解をおこない以下のように式変形します。(計算式は省略します)
$$V(s)=\frac{mg}{k} \frac{1}{s}+\frac{v(0)-\frac{mg}{k}}{s+\frac{k}{m}}$$
ここまで式変形ができたらそれぞれの項に対してラプラス逆変換の公式を当てはめます。そうすると\(v(t)\)は
$$v(t)=\{v(0)-\frac{mg}{k}\}e^{-\frac{k}{m} t}+\frac{mg}{k}$$
となります。
加速度の計算の時と同じように\(t=0\)の時と\(t=∞\)の時の数値を確認しておきましょう。
\(t=0\)の時\(v(0)=v(0)\)、\(t=∞\)の時\(v(∞)=\frac{mg}{k}\)となります。ここで、\(\frac{mg}{k}\)は終端速度と言われているものです。
\(ma = mg – kv\)の運動方程式において、加速度\(a=0\)のときの速度\(v\)とも一致しています。
位置
最後に位置について解いていきたいと思います。
運動方程式は以下の通りになります。
$$ma(t) = mg – kv(t)$$
今回は位置\(x\)に関して解くので、\(x\)を使って表すと以下のようになります。
$$m \frac{d^2x(t)}{dt^2}=mg – k\frac{dx(t)}{dt}$$
ラプラス変換を行うと以下のようになります。
\(t=0\)の時と\(t=∞\)の時の数値を確認しておきましょう。
\(t=0\)の時\(x(0)=x(0)\)、\(t=∞\)の時\(x(∞)=∞\)となります。
以上で解説は終了になります。お疲れさまでした!
スポンサーリンク


コメント