
Scilab(サイラボ)のXcosの連続時間システムで使用される11種類の関数(モジュール)を一覧にして整理しました。
公式サイトのオンラインヘルプは以下のリンクから確認することができます。(ほぼ英語)
【Xcosパレットカテゴリ一覧】
カテゴリ一覧の紹介です。リンクをクリックするとそのカテゴリの説明ページに移動します。(作成中)
| No | カテゴリ |
| 1 | 連続時間システム |
| 2 | 不連続 |
| 3 | 離散時間システム |
| 4 | ルックアップ・テーブル |
| 5 | イベント・ハンドリング |
| 6 | 数値計算 |
| 7 | 行列 |
| 8 | 電気工学 |
| 9 | 整数 |
| 10 | ポートとサブシステム |
| 11 | ゼロクロス検出 |
| 12 | 信号の配線 |
| 13 | 信号処理 |
| 14 | 暗示的 |
| 15 | 注釈 |
| 16 | 出力/表示 |
| 17 | 信号源 |
| 18 | 熱水力学 |
| 19 | ブロック・デモ |
| 20 | ユーザ定義関数 |
目次の項目をクリックすると選択した項目のページまで飛ぶことができます。
CLINDUMMY_f
 説明
説明
このブロックは,ゼロ交差ブロックを有するが, システムが連続系状態量を有さない場合, 全てのブロックダイアグラムに配置する必要があります. その理由は,ゼロ交差面を見つけるodeソルバです.
CLR
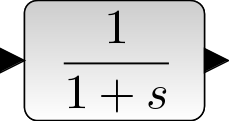
説明
このブロックは,有理伝達関数分子/分母 で表されたSISO線形系を実現します. 有理関数はプロパー (分母の次数が分子の次数以下)である必要があります.
ダイアログボックス
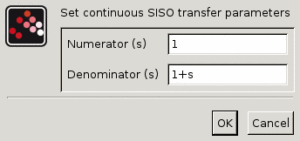
Numerator
このパラメータは伝達関数の分子を設定します.s の多項式を指定します.
プロパティ : 大きさ1の ‘pol’ 型.
Denominator
このパラメータは伝達関数の分母を設定します.s の多項式を指定します.
プロパティ : 大きさ1の ‘pol’ 型.
CLSS
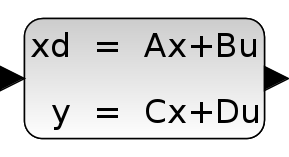
説明
このブロックは,連続時間線形状態空間システムを実現します.
![]()
ただし,x は状態変数ベクトル, u は入力関数ベクトル, y 出力変数ベクトルです.
システムは, (A, B, C, D) 行列と状態変数初期値 X0で定義されます. 次元は互換性を有する必要があります.
ダイアログボックス
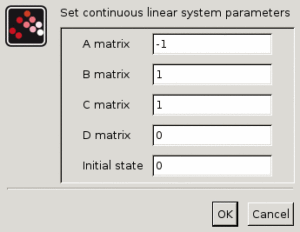
A 行列
正方行列.プロパティ : 大きさ [-1,-1]の’mat’型.
B 行列
B 行列, システムが入力を有さない場合は [] .プロパティ : 大きさ [“size(%1,2)”,”-1″] の ‘mat’型.
C 行列
C 行列 , システムが入力を有さない場合は [] .プロパティ : 大きさ [“-1″,”size(%1,2)”] の ‘mat’型.
D 行列
D 行列, システムがD項を有さない場合は [].プロパティ : 大きさ [-1,-1] の ‘mat’型.
状態変数初期値
系のベクトル/スカラー状態変数初期値.プロパティ : 大きさ “size(%1,2)” の ‘vec’型.
使用例
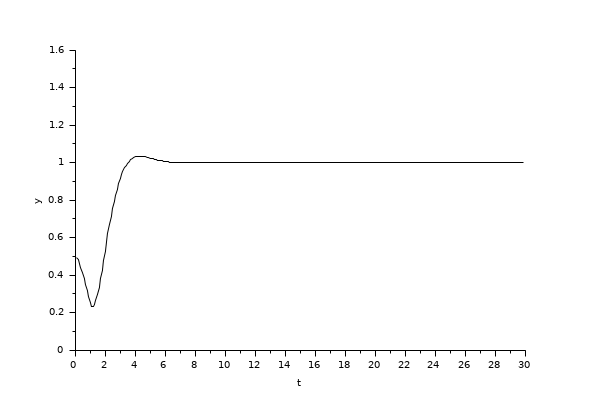
このサンプル例は,出力波形をシミュレート/表示するための以下に示す RLC回路y(t)=Vc(t)の 出力波形をシミュレート/表示するCLSSブロックの使用法を説明します.
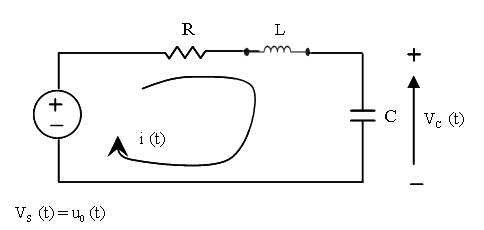
RLC回路の方程式を以下に示します. 結果はキルヒホッフの電圧則とニュートンの法則から得られます.
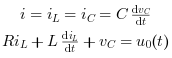
R, L および C はシステムの抵抗, インダクタンスおよびキャパシタ です.
キャパシタ電圧Vcとインダクタンス電流 iLを状態変数 X1 および X2として定義します.
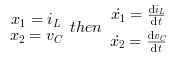
つまり
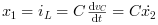
これらの方程式を整理することにより,以下を得ます:
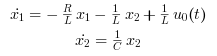
これらの方程式は 以下のような行列形式に変換できます,
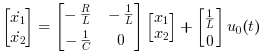
必要な出力方程式は
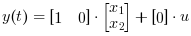
以下のダイアグラムはXcos上でモデル化されたこれらの方程式を示します. ただし, R= 10 Ω, L= 5 mΗ and C= 0.1 µF; 状態変数初期値は x1=0 および x2=0.5です.
出力 Vc(t) を得るために,連続時間システムパレットから CLSSブロックを使用します.
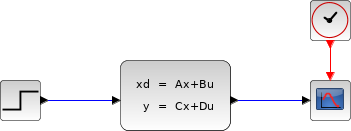
DERIV

説明
微分ブロックは入力の時間tに関する微分を計算します.
微分ブロックには設定はなく,ブロックの出力初期値はゼロです.
使用例
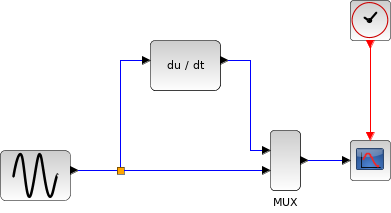
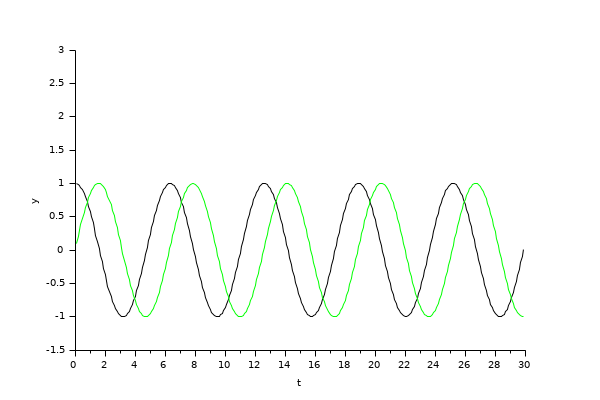
この例では,振幅2,周波数 1.25Hzの sin入力信号の微分波形を計算/表示します.
DERIVATIVEブロックの入力および出力波形を以下に示します:
INTEGRAL_f
説明
このブロックは積分器です. 出力は入力の積分です.
ダイアログボックス
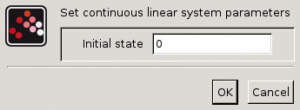
初期条件
初期条件を指定するスカラー.プロパティ : 大きさ1の’vec’型.
INTEGRAL_m

説明
このブロックは積分器です. 出力yは,カレント時間ステップtにおける 入力uの積分です.
ただし, y0 は初期条件, t0 は対応する時間です.
ダイアログボックス
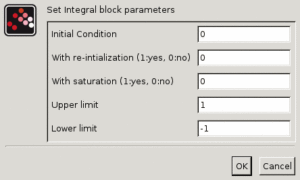 パラメータダイアログボックスにより以下を定義します:
パラメータダイアログボックスにより以下を定義します:
- 初期条件における飽和リミット指定の有無
- 積分の下限および上限リミット.
ダイアログボックスにより,指定した初期条件に 状態変数をリセットするためのイベントポートをブロック に追加できます.
“再初期化”を選択した場合, 以下が出力されます:
- 積分される値は積分ブロックポート番号1に接続できます. (積分ブロックの左上隅)
- 赤で記されたトリガーポートに トリガー信号を入力した際に積分が初期化される値は, 積分ブロックポート番号2に接続できます(積分ブロックの左下隅のポート).
初期条件
ベクトル/スカラー初期条件.
このパラメータにより,入力/出力のデータ型を定義できます. 実数または複素数型とすることができます.
プロパティ: 大きさ [-1,-1]の ‘mat’型.
再初期化有りの場合
状態量を外部信号に基づき指定した初期条件にリセットする場合, 1 を選択します.
プロパティ : 大きさ1の’vec’型.
飽和有りの場合
選択された場合, 状態変数は 下限飽和リミットおよび上限飽和リミットパラメータ の間の値に制限されます.
プロパティ : 大きさ1の’vec’型.
上限リミット
積分の上限リミット.
プロパティ : 大きさ[-1,-1]の’mat’型.
下限リミット
積分の下限リミット.
プロパティ : 大きさ[-1,-1]の’mat’型.
使用例
例1
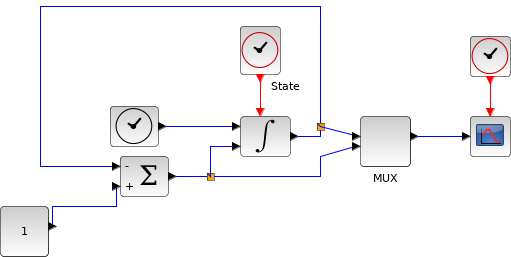
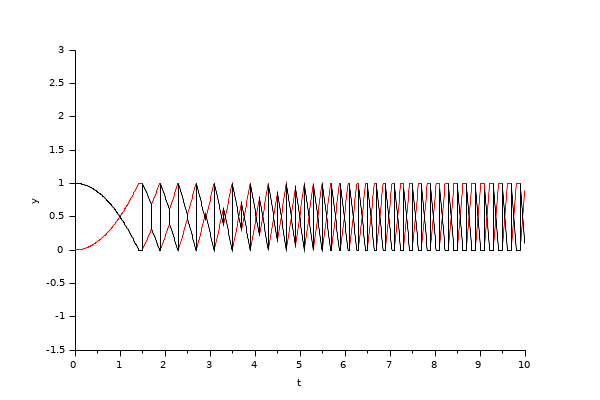
この例のモデルは積分器の状態ポートの使用例を示します.
再初期化パラメータを1, 上限リミットを 1, 下限リミットを -1に設定します.
例2
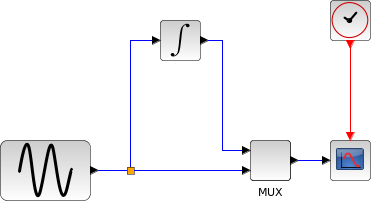
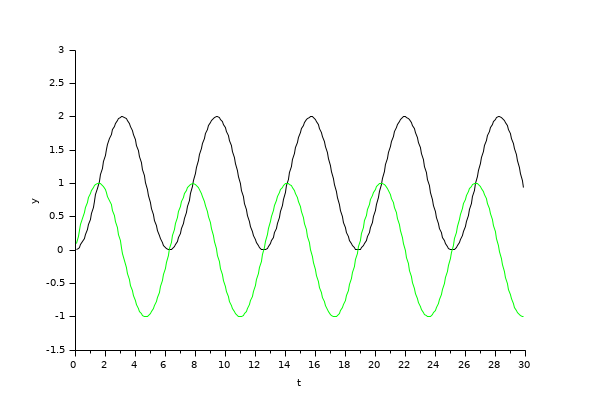
PID

説明
このブロックは PID (比例-積分-微分)制御器を実装します. “誤差”の値 Ue は,観測されたプロセス変数 Upr とセットポイント指令値 Ur の差から計算します.
Ue = Ur – Upr
制御目的は,プロセス変数 Up をセットポイント値 Urに追従させることです. PID制御器は,工業プロセスのフィードバック制御において 広く使用されています.
PID制御器の計算(アルゴリズム)には以下の3つのパラメータの値が含まれます; 比例 Kp, 積分 Ki, 微分 Kd. これらの項は,誤差信号Ueに適用する3種類の基本的な数学関数を 記述します. Kp はカレントの誤差への反応を定義, Ki は最近の誤差の合計への反応を定義, Kd は誤差の変化率への反応を定義します.
制御バルブまたは加熱要素の供給電力のような制御要素を通じて プロセスを調整するために, これらの3種類の処理の重み付き加算が使用されます. 従来のフィードバック制御系の基本構造を以下に示します:
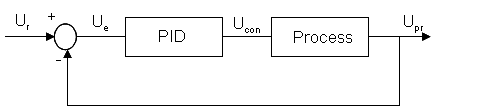
PID 則は入力変数 Up(t), その時間積分 Ui(t), その1階微分 Ud(t) の線形結合です. 制御則 Ucon(t) は以下の形式を有します:
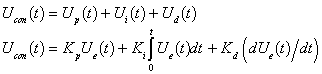
ダイアログボックス
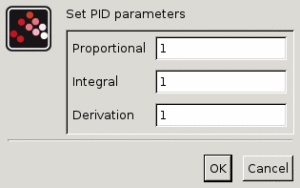
比例
誤差を乗じるゲインの値.
プロパティ : 大きさ-1の’vec’型.
積分
誤差の積分時間の値.(1/Integral)
プロパティ : 大きさ -1 の’vec’型.
微分
誤差の微分時間の値.
プロパティ : 大きさ-1の’vec’型.
使用例
例1
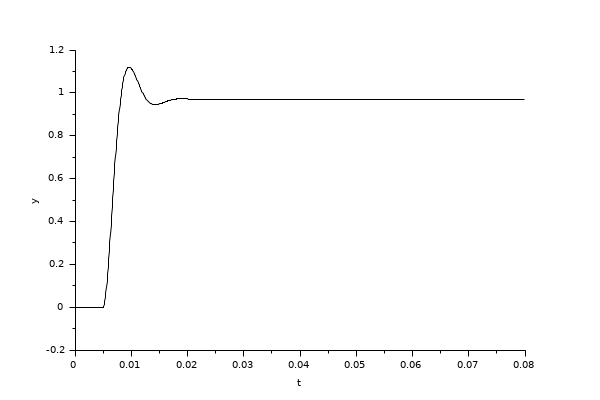
この例は,PIDレギュレータの使用例を示します. この制御は,簡単に出力信号 Upr(t) を指令信号 Ur(t) に一致させます.
この例では,制御系は, ダンピング係数 = 0.5, カットオフ周波数 fc = 100 Hzの 2次の単位ゲインローパスフィルタです. 伝達関数 H(s) を以下に示します:
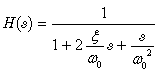
このフィルタをモデル化するには,連続時間システムパレットの 連続系伝達関数ブロック (CLR)を使用します.
PID パラメータ Kp, Ki および Kd を 100, 0.1 および 0に設定します.
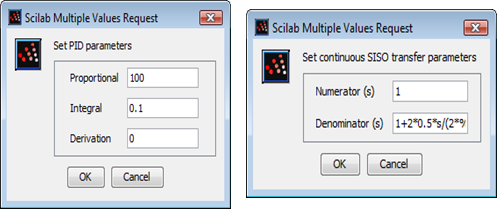
スコープはシステム誤差 Ue (黒), 基準信号 Ur (青) およびプロセス信号 Upr(赤) の波形を表示します. 最初,プロセス信号 Upr(t) が基準信号 Ur(t) に追従していないことが わかります.
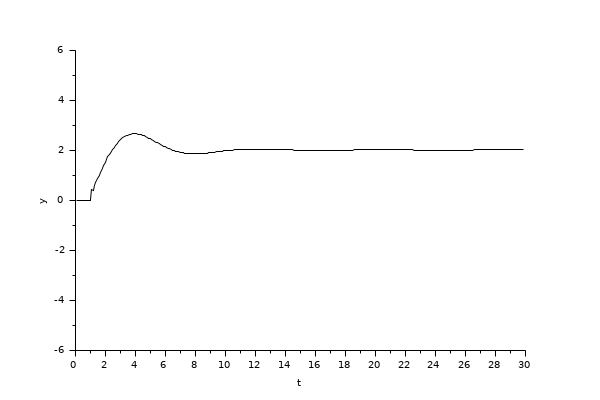
例2
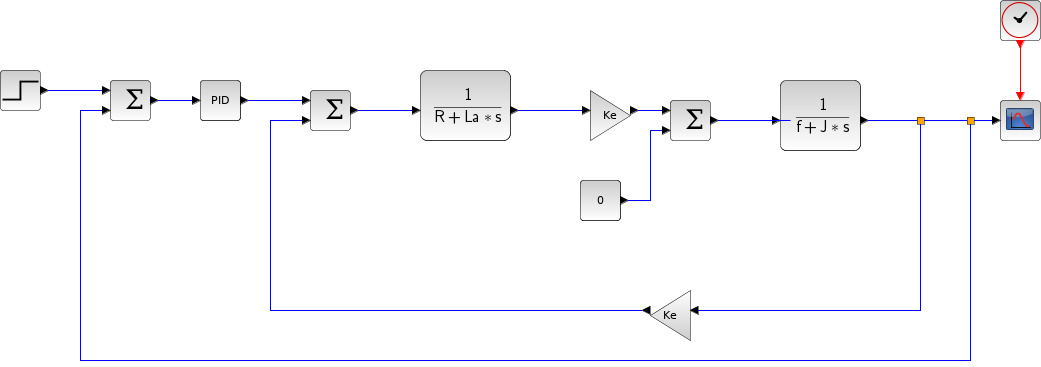
例3
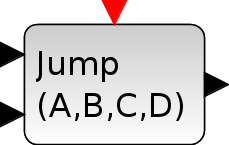
TCLSS
説明
このブロックは,状態量のジャンプを含む連続時間線形状態空間 システムを実現します.このブロックの入力の数は2つです. 最初の入力は線形システムの標準入力で,2番目の入力はこのブロックの 唯一のイベント入力ポートにイベントが発生した際に状態量にコピーされる 状態量の新しい値を保持します. これはシステムの状態量が(状態量の大きさに等しい)2番目の入力に現れる 値にジャンプすることを意味します. システムは,(A,B,C,D)行列と 初期状態量 x_0により定義されます. 次元は互換性を有する必要があります. 入力/出力の大きさは自動的に調整されます.
ダイアログボックス
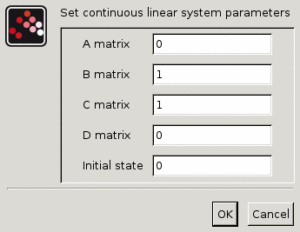
行列
A 正方行列.プロパティ : 大きさ [-1,-1]の’mat’型.
B 行列
B 行列, システムが入力を有さない場合は [].プロパティ : 大きさ [“size(%1,2)”,”-1″] の ‘mat’型.
C 行列
C 行列 ,システムが入力を有さない場合は [].プロパティ : 大きさ [“-1″,”size(%1,2)”] の ‘mat’型.
D 行列
D 行列, システムが D項を有さない場合は [].プロパティ : 大きさ [-1,-1]の’mat’型.
状態量初期値
システムの状態量初期値ベクトル/スカラー.プロパティ : 大きさ “size(%1,2)” の ‘vec’型.
使用例
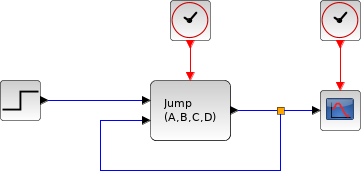

説明
伝送遅延ブロックは指定した時間だけ入力を遅延させます. このブロックは,時間遅延を模擬する際に使用できます. シミュレーション開始時に,このブロックは, シミュレーション時間が時間遅延パラメータを超え, ブロックが遅延した入力の生成を開始するまでの間, 初期値入力パラメータを出力します.
時間遅延パラメータは非負とする必要があります.
ダイアログボックス
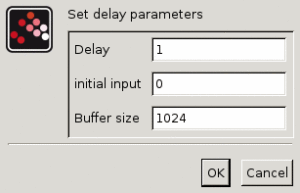
遅延
入力信号を出力に伝搬させる前に遅延させるシミュレーション時間の量. 値は非負である必要があります.
プロパティ : 大きさ1の ‘vec’型
初期入力
シミュレーション開始時と時間遅延の間にブロックで生成される出力.
プロパティ : 大きさ1の ‘vec’型
バッファサイズ
保存する点用に確保するメモリの初期値.
プロパティ : 大きさ1の ‘vec’型
使用例
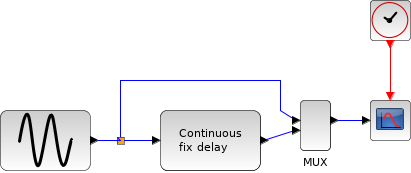
VARIABLE_DELAY

説明
可変伝送遅延ブロックは,ある作用とその効果の間の可変時間遅延を 模擬する際に使用できます. このブロックは,例えば,パイプを有するシステムで, パイプ内の流体をくみ上げるモータの速度が可変であるような場合に 使用できます.
このブロックは2個の入力と1個の出力を受け付けます: 最初の入力は信号 u(t) でブロックにより指定されます(データ入力); 2番目の入力は可変時間遅延 τ(t)です.
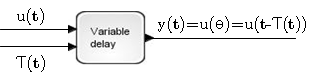
カレントの時間ステップtにおいて, このブロックは 遅延されたデータ入力 u(θ) を出力します. ただし,θはカレントのシミュレーション時間 t から 時間遅延パラメータ τをひいたものです.
出力信号の方程式は以下のようになります:
y(t) = y(θ) – u(t – τ(t))
ダイアログボックス
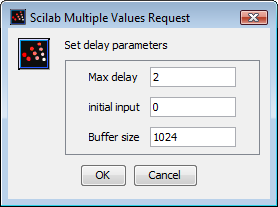
最大遅延
指定可能な時間遅延入力の最大値を定義します. この値を負にすることはできません.
プロパティ : 大きさ 1の’vec’型.
入力初期値
最初に時間遅延入力を超えるシミュレーション時間までに ブロックにより生成される出力. y(τ)に値が設定されない場合, t0における入力初期値とy(τ)の間で線形近似が 計算されます.
プロパティ : 大きさ1の’vec’型.
バッファの大きさ
ブロックが保存できる点の数.
プロパティ: 大きさ1の’vec’型.
使用例
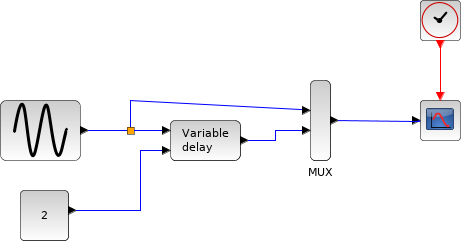
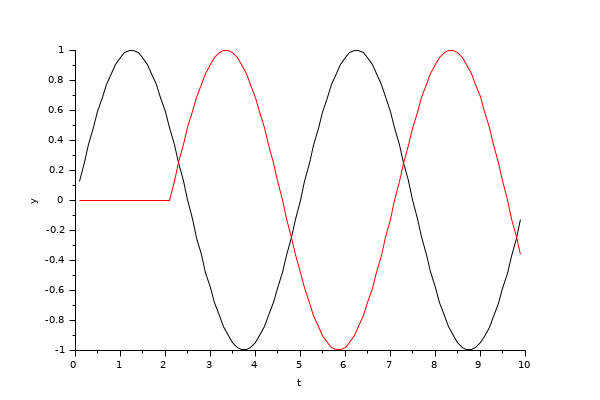
この例では, ブロックパラメータダイアログボックス内の 最大時間遅延に 4を指定します. 入力信号は振幅1,周波数0.2Hzのサイン波です.
2秒の遅延を導入するために定数ブロックに2を指定します. VARIABLE_DELAYブロックの入力および出力波形を以下に示します:
PDE

説明
このブロックは、Xcos内の1次元PDE(偏微分方程式)を解くためのいくつかの数値スキーム(有限要素(1次および2次)、有限差分(1次および2次)、有限体積(1次))の実装です。 数学的フレームワークは、時間と空間で最大次数2のPDE線形スカラーに制限されています。 目標は、解決するPDEをグラフィカルに説明できるXcosの使いやすいツールボックスをエンジニアや物理学者に提供することです。 決定システムは、PDEのタイプに応じて最も効率的な数値スキームを選択し、ソルバーを実行します。
ダイアログボックス
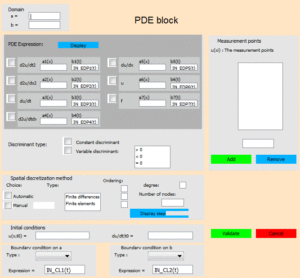
ドメイン
aおよびb:(double)離散化フィールドの2つのエッジ。
PDE仕様
- チェックボックスをオンにしてPDE演算子を選択します。 ai(x)、bi(t)(i = 1:7)は演算子係数です。
- 判別型:定数または変数。後者の場合、符号を付ける必要があります。
離散化方法
- 選択(チェックボックス):手動モードまたは自動モードの選択です。
- タイプ:手動モードでは、メソッドタイプ(有限差分、有限要素、有限体積)を指定できます。
- Degree:メソッドの程度(FDおよびFEメソッドの場合は1または2、FVメソッドの場合は1)。
- ノード数:節点の数を指定します。
初期状態
u(x、t0)=、du / dt at t0 =:初期条件を与えるため。
境界条件
- タイプ:境界条件には、ディリクレまたはノイマンの2つのタイプがあります。
- 式:境界条件式を与えます。
測定ポイント
測定ポイントのリストを提供します。
名前
ブロックの名前を与えるgetvalueボックス。
スポンサーリンク
 説明
説明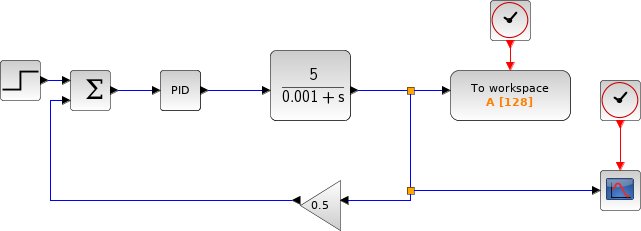

TIME_DELAY