この記事では慣性モーメントの計算方法を基礎から説明していきます。慣性モーメントの計算結果を覚えても良いのですが、それでは応用することができないので慣性モーメント求め方をマスターしていきましょう。
ちなみに慣性モーメントを計算する際には積分の知識が必要になってきます。積分に自信のない方は以下の記事も参考にしてみてください。
【数学】点⇒線⇒面⇒立体をイメージできれば積分で面積や体積を計算できる
スポンサーリンク
慣性モーメントとは
慣性モーメントと分かりやすく一言で説明するならば、ものの回転のしにくさの度合いと説明することができます。
回転させにくい要素は２つあります。
１つは重いもの、もう１つは回転軸から物体が離れているものです。
つまり、慣性モーメントは重さと軸からの距離で定義できることになります。
慣性モーメントは重さに比例する
まず重さについて考えてみます。
例えばボウリングのボールと野球のボールを床の上でクルクルと回転させようとしたとき、どちらが回転しにくいでしょうか？
答えはボウリングのボールですね。
これはボウリングのボールの方が重いからという理由です。
慣性モーメントは重さに比例して大きくなるという特徴があります。
慣性モーメントは軸からの距離の二乗に比例する
次に軸からの距離について考えてみます。
今度はボウリングボールを床の上でクルクル回す場合と、ボウリングボールにひもをつけてハンマー投げのように回転させる場合を考えてみましょう。
この場合ハンマー投げのように回転させる方が回転させにくいことが想像できると思います。これは同じ物体でも回転軸からの距離が遠くなればなるほど回転しにくくなることを意味しています。
慣性モーメントは距離の二乗に比例して大きくなるという特徴があります。
慣性モーメントの計算式
それでは実際に慣性モーメントを計算してみましょう。
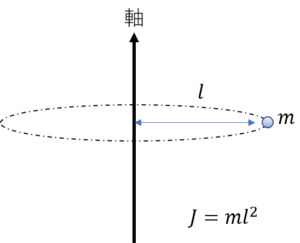
下の図のように回転させる軸があり、そこから\(l\)離れた場所に質量\(m\)の「物体」があります。
ここで「物体」という表現だと球なのか立方体なのか曖昧なので、理解をしやすくするために、この物体は「点」ということにしたいと思います。
また慣性モーメントを\(J\)とすることにします。
慣性モーメントは重さに比例し、軸からの距離の二乗に比例するので、以下のようになります。
$$J=ml^2$$
それでは一般的に慣性モーメントはどのように定義することができるでしょうか？
表現方法はいくつかありますので、たとえば以下のような表現方法を紹介します。
ここで、物体の密度をρとし質量\(m\)と体積\(V\)を用いて表すと\(ρ=\frac{m}{V}\)となります。
\((1)\)は質量\(m\)に軸からの距離の二乗\(x^2\)をかけたもの（点）を足し合わせるという意味です。今までの説明ではこの\((1)\)の式が一番わかりやすいのではないでしょうか？
\((2)\)は積分の形で表現しています。微小な質量\(dm\)と距離の二乗\(x^2\)をかけたものを足し合わせています。
\((3)\)は\((2)\)の\(dm\)を式変形しています。微小な重さというのは微小な体積×密度という風に分解できるので、このような計算式になります。
この記事では\((3)\)の計算式を使って慣性モーメントを計算してきたいと思います。
次以降の計算例で理解を深めていきましょう。
スポンサーリンク
慣性モーメントの計算例
線の慣性モーメント
まずは線（一様な棒）の慣性モーメントを計算してみたいと思います。
回転軸1
下の図のように長さ\(2l\)重さ\(m\)の線があります。この線の中心を回転軸として回転させるときの慣性モーメントを求めてみます。
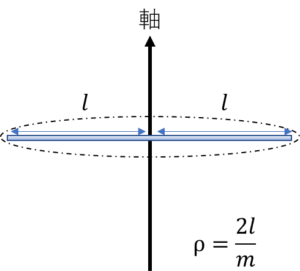
この線の密度ρは\(\frac{m}{2l}\)となります。
慣性モーメントは\(J=\int_{}{} x^2 ρdV\)で表されるのですが、ここでの\(dV\)は今回は\(dx\)になります。
\(dV\)は体積なのですが、今回は回転させる物体が「線」なので体積も一次元の線\(dx\)になります。
また、積分の範囲は\(-l\)から\(l\)になります。よって
となります。
回転軸2
今度は回転軸が棒の端とした場合の慣性モーメントを考えてみます。これは積分の範囲が変わることになりますので、
となります。
円盤の慣性モーメント
次に円盤の慣性モーメントを計算してみます。
円盤に関しては軸に対して平行な円盤と垂直な円盤の2種類について考えていきます。
回転軸１
下の図のように半径\(r\)重さ\(m\)の円があります。この円の密度ρは\(\frac{m}{πR^2}\)となります。
慣性モーメントは\(J=\int_{}{} x^2 ρdV\)であり、ここでの\(dV\)は軸から\(r\)離れた距離にある微小な面積になります。
つまり軸から\(r\)離れた円周\(2πr\)幅\(dr\)の面積と考えることができますので、\(dV\)は\(2πrdr\)になります。
また、積分の範囲は\(0\)から\(R\)になります。よって
回転軸２
次は下記のように回転する軸を変えてみたいと思います。先ほどと同様にこの円の密度ρは\(\frac{m}{πR^2}\)となります。
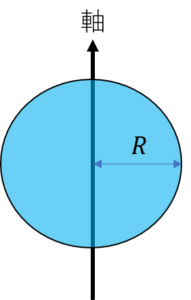
ここで、いきなり円盤の慣性モーメントを計算するのは難しいので、まずは下の図のように円盤の中に細い線があるとして、この細い線の慣性モーメント\(J_{1}\)を求めてみましょう。
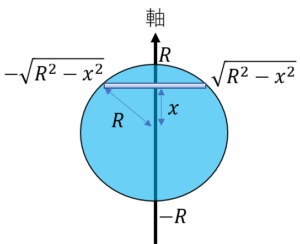
線の慣性モーメントの章で説明したように
$$ J_{1}=\int_{-\sqrt{R^2-x^2}}^{\sqrt{R^2-x^2}} y^2ρdy$$
と記述することができます。
これを整理すると
$$ J_{1}=\frac{2ρ}{3}(R^2-x^2)^{\frac{3}{2}}$$
となります。これは円盤の中の一部の線の慣性モーメントなので、これを\(-R\)から\(R\)まで積分したものが、求めたい円盤の慣性モーメントになります。よって、
$$ J=\int_{-R}^{R} \frac{2ρ}{3}(R^2-x^2)^{\frac{3}{2}} dx$$
$$ J=\frac{1}{4}mR^2$$
となります。※積分の過程は複雑なため積分ツールを用いて計算しています。
スポンサーリンク
円柱の慣性モーメント
円柱の慣性モーメントについてですが、これは先ほど円盤の慣性モーメントを計算したので、その結果を使って計算していきたいと思います。
薄い円盤の慣性モーメントは\(\frac{1}{2} m_{1} R^2\)でした。これが高さ\(h\)分積み重なったとものが円柱の慣性モーメントと考えることができます。
ただし、重さの定義には注意が必要です。円柱の重さを\(m\)とすると、薄い円盤の重さ\(m_{1}\)は\(\frac{m}{h}\)となります。
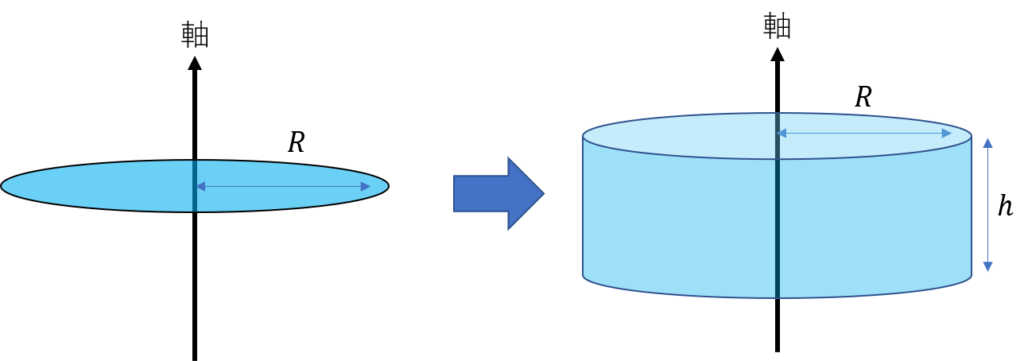
よって、円柱の慣性モーメントは以下のようになります。
$$J = \int_{0}^{h} \frac{1}{2} \frac{m}{h}R^2 dx $$
$$J=\frac{1}{2} mR^2$$
高さ\(h\)が消えているのに気づいたかと思いますが、この結果は円盤と円柱の慣性モーメントは等しいということを意味しています。ただし、円盤と円柱の重さが等しいことが前提になります。
つまり、重さが等しいならば高さに依存しないため、薄い円盤でも、厚みのある円柱でも慣性モーメントは同じということになります。
球の慣性モーメント
球の慣性モーメントは円盤の慣性モーメントが足し合わせることで求めてみたいと思います。球の密度ρは\(\frac{3m}{4πR^3}\)となります。
円盤の慣性モーメントは\(\frac{1}{2} m_{1}R_{1}^2\)なのですが、球を輪切りにして無数の円盤があると考えた時に、それぞれの円盤の半径\(R_{1}\)と\(m_{1}\)はどのように変わるか考えてみます。
まず\(R_{1}\)がどのように変わるかについてですが、\(R_{1}\)の動かす方向を\(-R\)から\(R\)とし、動かす変数を\(x\)とすると
$$R_{1}=\sqrt{R^2-x^2}$$
となります。
また、円盤の重さ\(m_{1}\)についてですが、これは密度×面積で表すことができるので、
$$m_{1} = ρ×π{\sqrt{R^2-x^2}}^2$$
となります。
よって、円盤の慣性モーメント\(\frac{1}{2} m_{1}R_{1}^2\)を足し合わせたものが球の慣性モーメントになるので、
$$J = \int_{-R}^{R} \frac{1}{2} ρπ{\sqrt{R^2-x^2}}^2 {\sqrt{R^2-x^2}}^2 dx $$
$$J = \int_{-R}^{R} \frac{3m}{8R^3} (R^4-2R^2x^2+x^4) dx $$
$$J = \frac{2}{5} mR^2 $$
となります。
直方体の慣性モーメント
直方体の慣性モーメントを考えていきたいと思いますが、まずは長方形の慣性モーメントを考えてみることにしましょう。
図のように\(x\)軸方向に\(2a\)、\(y\)軸方向に\(2b\)の長方形があります。この長方形を\(z\)軸周りに回転させることを考えてみます。この長方形の密度ρは\(\frac{m}{4ab}\)となります。
慣性モーメントは\(J=\int_{}{} x^2 ρdV\)と表されるのですが、今回は立体ではなく面なので、\(dV\)は\(z\)軸から離れた微小な面積になります。
また、\(z\)軸からの微小な面積までの距離は\(\sqrt{x^2+y^2}\)となりますので、
$$ J=\int_{-b}^{b} \int_{-a}^{a} {\sqrt{x^2+y^2}}^2ρdxdy$$
$$ J=ρ\int_{-b}^{b} (\frac{2}{3} a^3+2ay^2)dy$$
$$ J=ρ(\frac{4}{3} a^3b+\frac{4}{3} ab^3)$$
$$ J=\frac{1}{3}m(a^2+b^2)$$
となります。
ここで直方体の慣性モーメントですが、長方形の慣性モーメントを\(z\)軸方向に積み重ねていけば、直方体の慣性モーメントになります。
これは円柱の慣性モーメントの章で説明したように、直方体の高さによらず一定になります。よって、直方体の慣性モーメントも
$$ J=\frac{1}{3}m(a^2+b^2)$$
となります。
ただし、長方形と直方体の重さが同じということが前提になることに注意が必要です。
スポンサーリンク
慣性モーメント計算手順まとめ
以上5種類の物体の慣性モーメントの求め方を紹介しました。慣性モーメントのおおまかな計算手順を整理しておきたいと思います。
①物体の密度を計算する
まずは物体の密度を計算しておきましょう。手順としてはほぼ必須となりますので、最初に計算しておくことをおすすめします。
②物体がどのような線や面でできているかをイメージする
物体がどのような線や面で構成されているか意識してみましょう。例えば長方形であれば線が集まって構成されており、円柱であれば円が積み重なってできたものになります。
③線や面の慣性モーメントを計算する
②で線や面のイメージができたら、今度はその線や面の慣性モーメントを計算してみましょう
今回は慣性モーメントを下記の式で計算しました。微小な体積\(dV\)をケースバイケースで数式で記述できるようにしましょう。
$$ J=\int_{}{} x^2 ρdV \tag{3}$$
④③で計算した慣性モーメントを足し合わせる
最後は③で計算した慣性モーメントを足し合わせます。例えば薄い円盤の慣性モーメントが分かっていれば、それを積み重ねれば円柱の慣性モーメントになる例を紹介したように、細かく分割した慣性モーメントを足し合わせるということも覚えておきましょう。
以上で説明を終わります。お疲れさまでした！
スポンサーリンク
コメント