
なぜ積分すると面積や体積が計算できるのかイメージが良く分からない方もいるかと思います。ここでは、積分の理解を深めるためにために点⇒線⇒面⇒立体というイメージを使って説明していきたいと思います。
スポンサーリンク
積分の定義
いきなり数式になりますが、積分の定義としては以下の定義で表されます。この意味をまず考えてみたいと思います。
これはmin(最小値、下限)からmax(最大値、上限)の間で\(f(x)\)の関数を細かく区切って足し合わせるという意味になります。実際の例題として立方体の体積を算出する例で説明していきます。
点から線
線は点の集合体
立方体の体積を算出する前にまず線の長さを測定することを考えてみましょう。
ここでは、線の長さは短い線(点)がいくつも集合したものと考えます。
例えば1mの細い線があったときにこれは0.1mの線が10本あると見ることもできますよね。
このように小さいな細い線を非常に小さくしたものを\(dx\)ということにします。
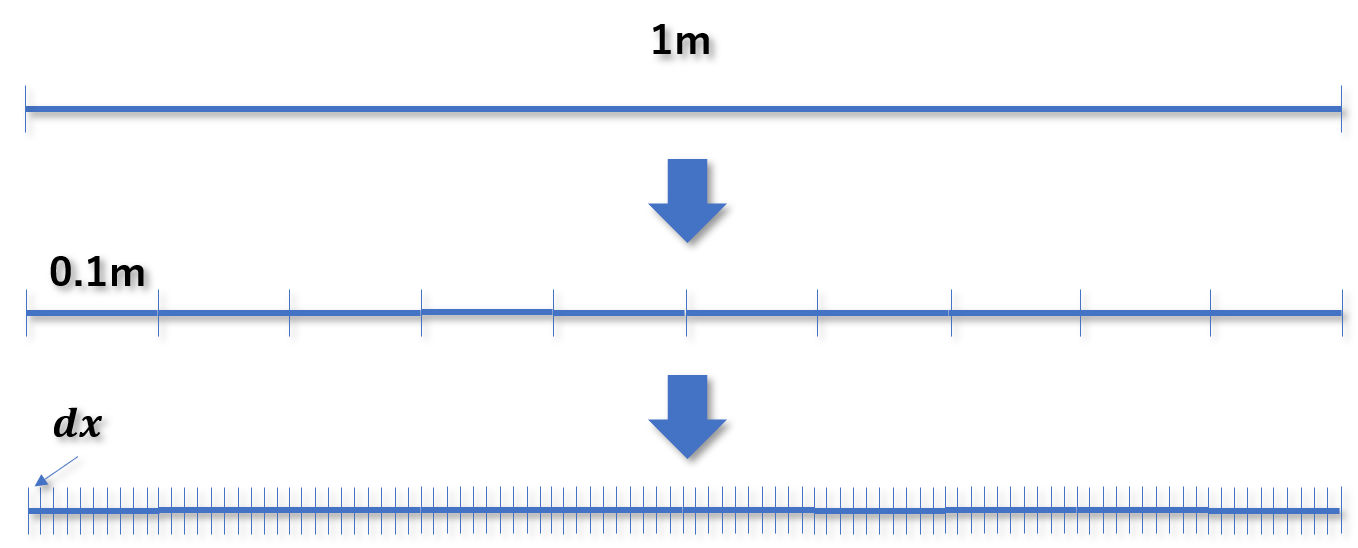
よって、この限りなく\(dx\)を限りなく小さくしていくと1メートルの長さは以下のように分解することができます。
$$ 1 = 10×0.1 $$
$$ 1 = 100×0.01 $$
$$ 1 = 1000×0.001 $$
$$ {…} $$
$$ 1 = ?×dx - ①$$
最終的に①のようになるのですが、\(dx\)はものすごく小さい長さ(点)なので、「?」には何を入れてよいか迷ってしまいます。
そこで積分記号\(\int\)が出てきます。線の長さは\(dx\)を0から1の範囲まで足し合わせればよいので、①は以下のように記述することができます。
$$ 1=\int_0^1 dx$$
実際にこの右辺を積分して計算すると
$$ \int_0^1 dx = [x]_0^1 $$
$$ =1-0 = 1 $$
結果は1となり当然ですが線の長さと一致します。
このように線の長さは小さな\(dx\)の和で表されることになります。
【補足】
ここで積分の定義式をもう一度確認すると以下のような式になっています。
$$\int_{min}^{max} f(x) dx $$
\(min\)は0、\(max\)は1ですが、\(f(x)\)は一体何になるのでしょうか?
正解は1なのですが、どういう意味かをしっかり理解することが重要です。
\(f(x)\)は\(x\)が0から1まで変化する間に足し合わせたいもの(今回は\(dx\))がどのように変化するかをイメージすると分かりやすいと思います。
今回の場合は\(dx\)は均等に分割されているので、0から1のどの場所の\(dx\)を見ても同じ(1倍されている)ことになります。
よって\(f(x)=1\)となるわけです。
例えば1mの線を10分割すると\(dx\)は0.1となるので、
$$1 = 0.1+0.1+…+0.1$$
となりすべての\(dx\)は0.1となり\(dx\)が1倍されていることになります。\(dx\)がものすごく小さな値だとしてもこれは同じ結果(1倍)になります。
線から面
面は線の集合体
線の長さが\(dx\)の和で表現されることを理解できたところで、次は面積について考えていきたいと思います。
面は線が集まってできたものと考えることができます。
例えば1m×2mの薄い紙があったとします。これの面積は2㎡です
この薄い紙は1m×0.2mの薄い紙が10個あると見ることもできますよね。
このように区切る単位を非常に小さくしたものを\(dy\)ということにします。
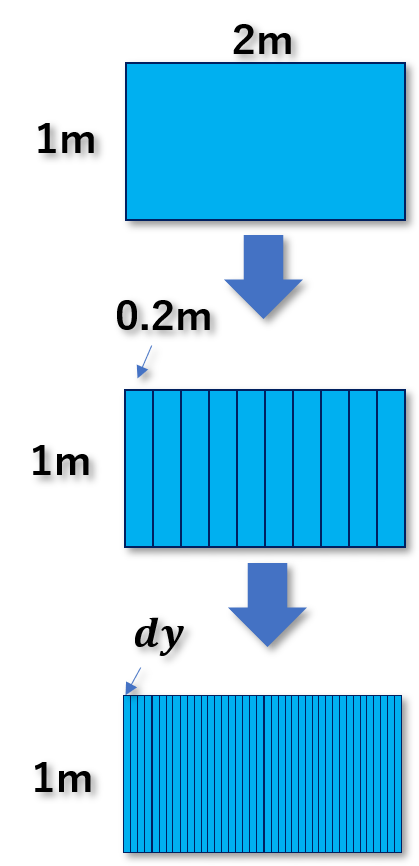
よって、この限りなく\(dy\)を限りなく小さくしていくと1m×2mの薄い紙の面積(2㎡)は以下のように分解することができます。
$$ 2 = 1×(10×0.2) $$
$$ 2 = 1×(100×0.02) $$
$$ 2 = 1×(1000×0.002) $$
$$ {…} $$
$$ 2 = 1×?×dy - ②$$
最終的には②のようになり、これは積分記号を用いてこのように記載することができます。
$$ 2=1×\int_0^2 dy$$
実際にこの右辺を積分して計算すると
$$ 1×\int_0^2 dy = 1×[y]_0^2 $$
$$=2-0= 2$$
結果は2となり薄い紙の面積と一致します。
面積も線の長さ×小さな\(dy\)の和で表されることになります。
スポンサーリンク
面から立体
立体は面の集合体
次に立体の説明です。ここまでくれば面が立体になることは想像できるのではないでしょうか?
立体は面が集まってできたものと考えることができます。
例えば1m×2m×3mの立方体があったとします。この立方体の体積は6㎥です
この立方体は1m×2m×0.3mの立方体が10個あると見ることもできますよね。
このように区切る単位を非常に小さくしたものを\(dz\)ということにします。
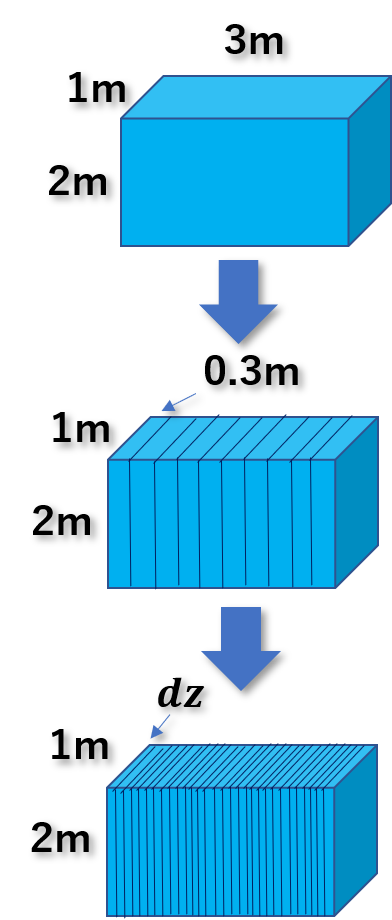
よって、この限りなく\(dz\)を限りなく小さくしていくと1m×2m×3mの立体の体積(6㎥)は以下のように分解することができます。
$$ 6 = 1×2×(10×0.3) $$
$$ 6 = 1×2×(100×0.03) $$
$$ 6 = 1×2×(1000×0.003) $$
$$ {…} $$
$$ 6 = 1×2×?×dz - ③$$
最終的には③のようになり、これは積分記号を用いてこのように記載することができます。
$$ 6=1×2×\int_0^3 dz$$
実際にこの右辺を積分して計算すると
$$ 1×2×\int_0^3 dz = 1×2×[z]_0^3 $$
$$ =6-0= 6 $$
結果は6となり立方体の体積と一致します。
以上で体積は面積×小さな\(dz\)の和で表されることになります。
点⇒線⇒面⇒立体をまとめると
今までの説明で小さな線(点)の単位を\(dx\),\(dy\),\(dz\)とあえて違う表現をしました。これは基本的には意味は同じなのですが、小さな単位を並べる方向が違うので、\(x\),\(y\),\(z\)と3つの方向を表すためにこのように3種類の記号を使用しました。
ここで体積を\(V\)として今までの結果をまとめると以下のような式になります。
$$V = \int_0^3\int_0^2\int_0^1 dxdydz$$
まずは\(x\)について積分を行い線の長さを計算します。次に線の長さ×\(dy\)の積分を行い面積を計算します。最後に面積×\(dz\)の積分を行い体積を計算する流れになります。このように考えると積分は点⇒線⇒面⇒立体ということがイメージできるのではないでしょうか?
次の記事では実際に例題で面積や体積を計算しますので、そこでさらに理解を深めてみましょう。
【数学】積分を使って面積や体積を計算する方法を分かりやすく解説
スポンサーリンク


コメント