
なぜ積分を使うと面積や体積が出せるのかということを理解していただくために、ここではいくつかの例題を使って積分の理解を深めていきたいと思います。三角形と円の面積を求める例題と円柱、三角錐、球の体積を求める例題を紹介します。
前回の記事で積分のイメージを説明していますので、積分の理解に自信のない方はこちらの記事もどうぞ
【数学】点⇒線⇒面⇒立体をイメージできれば積分で面積や体積を計算できる
スポンサーリンク
面積を求める例題
まずは面積を求める例題から説明します。面積を求めるときのポイントはどのような線が集まって面を形成しているかをイメージすることが大切です。
三角形
下の図のように\(y=x\)の直線があり、原点,\((1,0)\),\((1,1)\)の3点を結ぶ三角形の面積\(S\)を求めてみたいと思います。
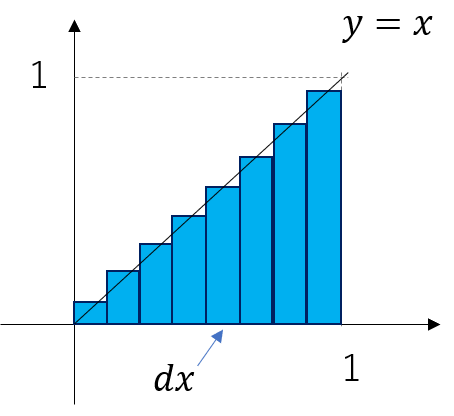
まずこの三角形がどのような細い線で形成されているかを考えてみます。
今回は\(x\)軸から無数の細い線が出ているとし、細い線の幅を\(dx\)とします。積分する範囲は\(x\)軸方向に0から1となります。
また細い線の長さ\(y\)は\(x\)に比例して大きくなっていきます。(\(y=x)\)
つまり求めたい細いは幅\(dx\)に長さ\(y\)をかけたものになるので、\(xdx\)となります。
よって、面積\(S\)は以下のようになります。
$$S = \int_0^1 xdx$$
$$ = \left[ \frac{ x^2 }{ 2 } \right]_0^1$$
$$ = \frac{ 1 }{ 2 }$$
円
円は2通りの求め方を紹介します。ここで求めたい円の面積の半径を\(R\)としておきます。
パターン①
1つ目の求め方についてです。
円の面積を求めたいので、円がどのような線の集まりでできているかを考える必要があります。
例えば円の中心に小さな円を描き、その円よりも少しだけ大きい円を外側に描き、さらにその円よりも少しだけ大きい円を外側に描く、といったことをずっと繰り返すと最終的には円の中が線でいっぱいに満たされます。
このように内側から円を描いていって面を作る方法で面積を計算してみます。
下の図のように中心から\(r\)離れた位置に小さな幅\(dr\)の円があるとします。
この円の周の長さは\(2πr\)になります。
この円を引き伸ばすと、細い線になりこれは\(dr×2πr\)と表すことができます。

よって、内側から外側にかけてこの細い線\(dr×2πr\)を足し合わせていったものが円の面積になるので、円の面積\(S\)は以下のようになります。
$$S = \int_0^R 2πrdr$$
$$ = 2π\left[ \frac{ r^2 }{ 2 } \right]_0^R$$
$$ = πR^2$$
パターン②
次に紹介する求め方は、円が下図のように縦の細い線の集まりでできていることイメージした方法で面積を計算します。
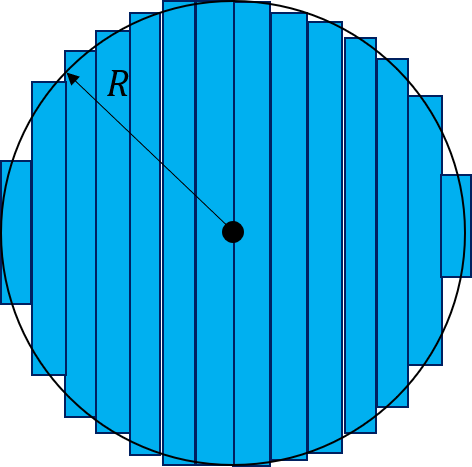
円が下図のように配置されていたとして、求めたい細い線をまずは定義してみます。
求めたい細い線は下の図でいうと青い細い線になります。

半径\(R\)で\(x\)軸上の\(x\)地点の細い線は、三平方の定理より\(2{\sqrt{ R^2-x^2}}\)となりこれに幅\(dx\)をかけたものが求めたい細い線になります。
また、今回積分する範囲は\(-R\)から\(R\)までなので、円の面積\(S\)は以下のようになります。
$$S = \int_{-R}^{R} 2{\sqrt{ R^2-x^2}}dx$$
$$ = πR^2$$
※この積分は少々難しく、置換積分という方法を用いて解く方法が一般的です。解法は省略しますが、まずは計算式を組み立てれるようになることを最初のステップとしましょう。
スポンサーリンク
体積を求める例題
次は体積を求める例題です。体積を求めるときのポイントはどのような面が集まって立体を形成しているかをイメージすることが大切です。
円柱
下の図のように半径\(R\)高さ\(h\)の円柱の体積\(V\)を求めてみたいと思います。
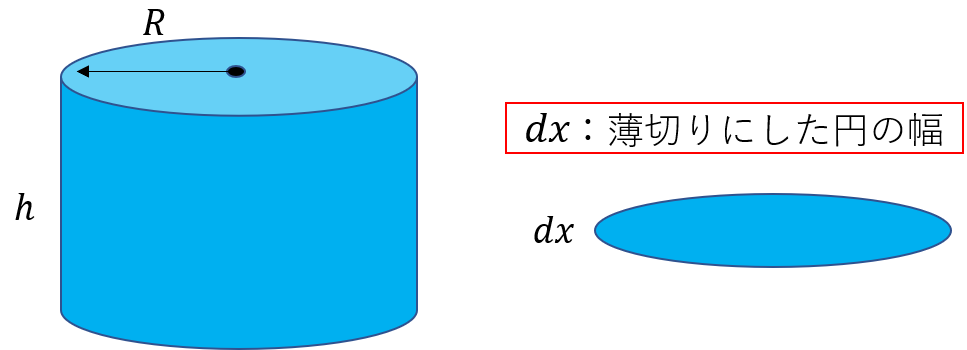
まず円柱を薄切りにした円を考えてみます。そうすると円柱はこの薄い円がたくさん集まったものと考えることができます。
また、このときの薄い円の幅を\(dx\)とします。すると円の面積\(S\)は
$$S = πR^2$$
となります。よって求めたい円は面積と幅を掛け算して、\(πR^2 dx\)となります。
あとはこの円が高さ\(h\)だけ集まっていることになりますので、体積\(V\)は
$$V = \int_0^h πR^2 dx$$
$$ = πR^2 h$$
円柱の体積の公式である底面積×高さと一致することが分かります。
三角錐
次は下の図のような三角錐の体積\(V\)を求めてみたいと思います。

まず積分する方向を今回は\(z\)軸方向と決めたいと思います。よって\(z\)は0から1の範囲で積分することになります。
また、この三角錐は\(xy\)平面と平行に切り取った薄い三角形がたくさん集まったものと考えることができます。
ここまでは円柱の体積と同じだったのですが、三角錐で違うところが\(z\)が変化すると薄い三角形の面積も変わってくるということです。
\(z\)が0のとき三角形の2辺は長さ1で、\(z\)が1のときは三角形の2辺の長さは0になります。
これを数式で表すと三角形の2辺の長さは\((1-z)\)と表すことができます。
よって三角形の面積\(S\)は
$$S = \frac{ 1 }{ 2 } (1-z)^2 $$
となり薄い三角形の幅を\(dz\)とすると体積\(V\)は以下のようになります。
$$V = \int_0^1 \frac{ 1 }{ 2 } (1-z)^2dz$$
$$ = \frac{ 1 }{ 2 } \left[ -\frac{ (1-z)^3 }{ 3} \right]_0^1$$
$$ = \frac{ 1 }{ 6 }$$
ここで補足ですが、体積\(V\)を導出するときに面積の式に\(z^2\)という項が現れます。
これを積分すると\(\frac{ 1 }{ 3 }\)という係数がでてきます。〇〇錐という立体の体積は底面積×高さ×\(\frac{ 1 }{ 3 }\)と覚えている方も多いと思いますが、\(\frac{ 1 }{ 3 }\)という係数はここの導出過程から出てくるものです。
球
最後に球の体積についてです。半径\(R\)の球の体積を求めてみたいと思います。

今回は\(yz\)平面に平行な面で球を切断することとします。そうすると薄い円が現れます。ゆで卵を輪切りにしたものを想像してもらえると分かりやすいと思います。
この薄い円がたくさん集まったものが球と考えることができます。
ここで円の面積を計算した時と同様考え方をしてみます。
 この図は\(y\)軸方向から球をみたものになります。。求めたい薄い円の半径は\({\sqrt{ R^2-x^2}}\)となります。
この図は\(y\)軸方向から球をみたものになります。。求めたい薄い円の半径は\({\sqrt{ R^2-x^2}}\)となります。
よってこの薄い円の面積\(S\)は\(π( R^2-x^2)\)となります。
また、今回積分する範囲は\(-R\)から\(R\)までなので、球の体積\(V\)は以下のようになります。
$$V = \int_{-R}^{R} π( R^2-x^2)dx$$
$$ = π\left[ R^2 x -\frac{ x^3 }{ 3 } \right]_{-R}^{R}$$
$$ = \frac{ 4πR^3 }{ 3 }$$
となります。次の記事では積分を使って球の表面積を導出することを考えてみたいと思います。
スポンサーリンク


コメント